探索地幔对流的奥秘——东京大学地震研究所春之学校2024总结报告（实践篇）

在理论篇中，我介绍了地幔对流的基本概念和基础方程式，并且介绍了瑞利数的物理意义。在实践篇中，我将着重介绍此次春之学校中通过数值模拟方法实际计算出的地幔对流结果，并围绕这些结果阐述瑞利数、计算区域形状、岩石相变等对地幔对流的影响。

目录隐藏

1 最简单的情况——不同瑞利数下的矩形区域内的对流

2 更为贴近地球的情况——不同瑞利数下的扇形区域内的对流

3 再现地幔对流——同心圆区域内的对流

4 更加复杂的对流模拟——从矿物学的角度来看对流

5 如何再现出更加真实的对流？

6 参考文献

最简单的情况——不同瑞利数下的矩形区域内的对流

为了初步了解瑞利数和对流之间的关系，我们决定首先参照Blankenbach, et al. (1989)的方案考虑最为简单的情况，即不同瑞利数下的矩形区域内的对流。

如图6所示，我们首先考察了瑞利数为100、1000、10000和100000的矩形区域内对流。可以看出，瑞利数极小（100）的情况下，矩形区域内基本未发生对流，热基本是通过热传导进行传播的。而瑞利数达到1000左右后，矩形区域内开始出现了对流现象。其中，瑞利数越大，则对流发生得越激烈。

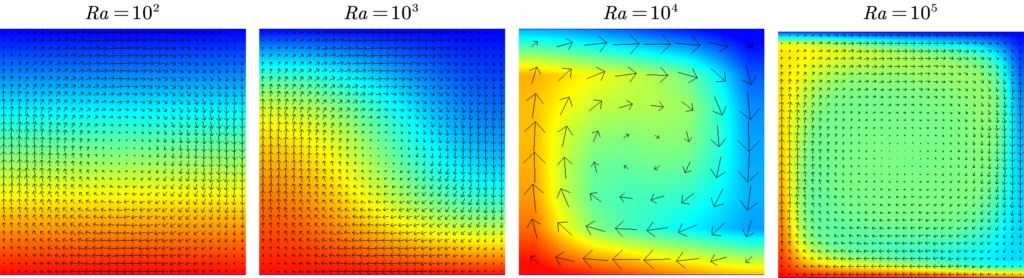
图6 不同瑞利数下的矩形区域内的对流。其中，红色代表该区域内的温度较高，蓝色代表该区域内的温度较低；黑色箭头代表归一化后的流线。

为了比较不同瑞利数下发生的对流的激烈程度，我们决定通过沿竖直方向求出水平方向上的平均温度的方式考察温度分布。如图7所示，在瑞利数仅有100的情况下，温度与竖直方向上的坐标成正比例关系。这印证了我们刚才得出的结论，即矩形区域内的热基本都是通过热传导进行传播的。而瑞利数逐渐增大后，竖直方向上的温度分布逐渐发生变化。其中，在瑞利数达到10000和100000时，甚至在矩形区域的中心区域（ $0.1<z<0.9$ ）出现了温度梯度发生逆转的情况。这种逆转情况意味着对流发生得十分激烈。

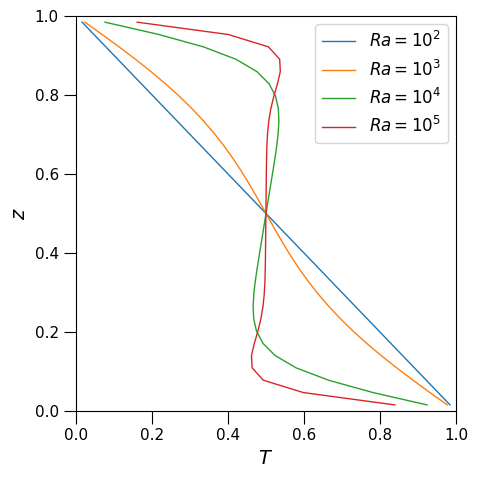
根据森重先生的介绍，在地球科学领域里研究者们经常通过比较温度剧烈变化的区域来评估对流的激烈程度。这种温度急剧变化的区域被称为温度边界层（temperature boundary layer）。例如，在图7中， $Ra = 10^4$ 时 $0.0<z<0.2$ 和 $0.8<z<1.0$ 的区域，以及 $Ra = 10^5$ 时 $0.0<z<0.1$ 和 $0.9<z<1.0$ 的区域就属于温度边界层。一般而言，温度边界层的范围越小，则说明对流发生得越激烈。

综上所述，我们通过最简单的情况，可以得出瑞利数越大，则温度边界层范围越小，对流发生得越激烈的这一重要结论。

更为贴近地球的情况——不同瑞利数下的扇形区域内的对流

对于现代人而言，绝大多数人都认可“地球是球体”这一基本事实。因此，如果我们想要模拟出更大规模的地幔对流，我们需要将研究对象从矩形区域扩张至扇形区域。对此，我们制作了这样的研究区域：地表至地幔之间的距离为地幔至地球重心之间的距离的1.2倍的二维扇形模型。除了研究区域发生变化之外，热传递所遵循的基本方程式不变。

为了与上述的矩形区域内的对流进行比较，我们仍然将瑞利数设置为100、1000、10000和100000并进行了数值模拟。最终，我们获得了如图8所示的对流图像。可以发现，瑞利数较小（100和1000）的情况下，扇形区域内的热传递与矩形区域的情况基本一致。然而，在瑞利数达到10000时，虽然扇形区域内也发生了明显的对流，但与矩形区域的情况相比，扇形区域内的整体温度都较低。此外，当瑞利数为100000时，由于算法的不足，我们未能获得收束的计算结果。

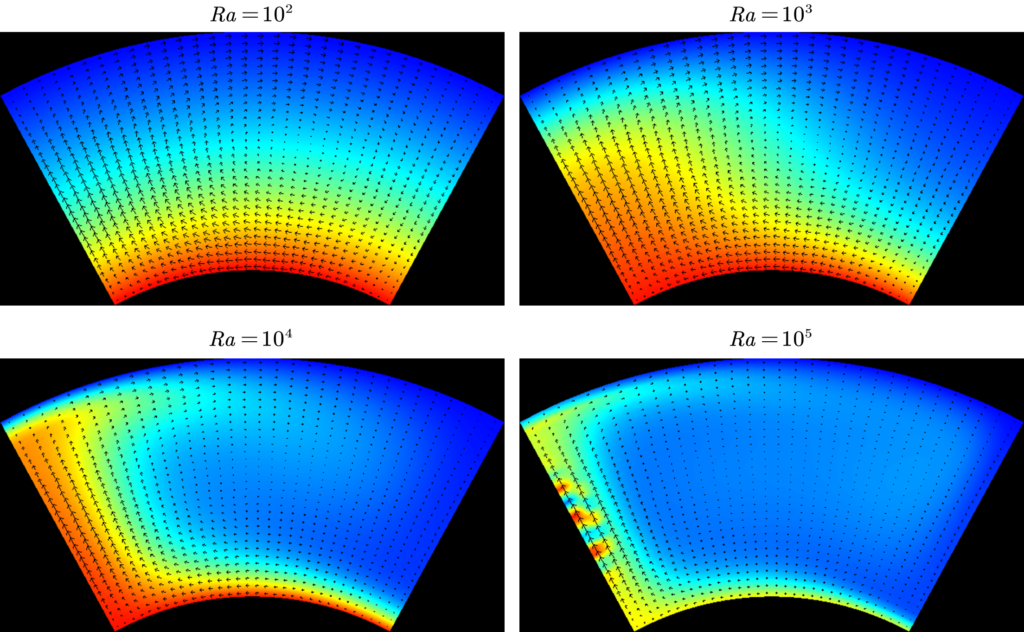
图8 不同瑞利数下的扇形区域内的对流。其中，红色代表该区域内的温度较高，蓝色代表该区域内的温度较低；黑色箭头代表归一化后的流线。需要注意的是，瑞利数为100000时的计算结果未能收束。

同样地，如果我们沿径向计算平均温度分布，可以得到如图9所示的图像。通过与连接了(0, 1)和(1, 0)两点的直线进行比较，可以发现无论瑞利数有多大，径向的平均温度分布整体都偏低。这是因为在我们设定的扇形区域模型中，由于代表地表（ $z = 1.0$ ）的曲线长度比代表古登堡面（ $z = 0.0$ ）的曲线长度大一些，因此古登堡面的热源造成的加热效果比地表的“冷源”造成的冷却效果要小。这种冷却效果随着热传导和对流不断影响着扇形区域内的各处，最终导致扇形区域内的温度整体偏低。

图9 不同瑞利数下的扇形区域对流的径向平均温度分布。其中，红色虚线为连接了(0, 1)和(1, 0)两点的直线。

即便如此，从图9可以看出，在瑞利数较大（10000）时仍然出现了温度边界层。这说明在扇形区域模型里，随着瑞利数的增大，对流也会发生得更加激烈。

再现地幔对流——同心圆区域内的对流

正如我在理论篇中介绍的一样，地球内部可以被分为地壳、地幔、外核、内核这4个规模巨大的圈层。由于地幔处于地球内部相对靠外的地方，因此它可以被2个同心球之间的区域粗略地描述。不过，由于对三维空间进行数值模拟是一项计算量十分巨大的事情，因此我们决定沿用之前的做法，即仅考虑二维空间的2个同心圆之间区域的对流情况。

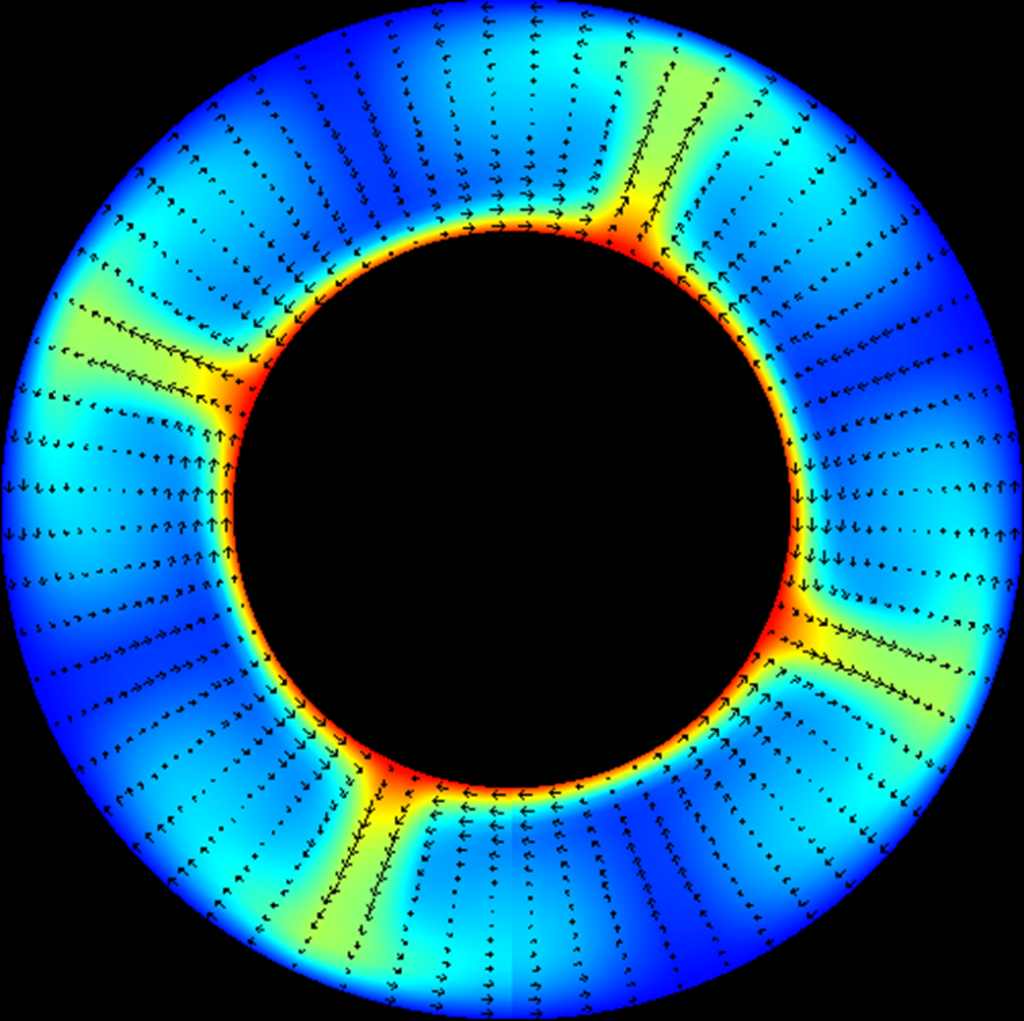
虽然在理论篇中，我们概算出了地幔的瑞利数的数量级为 $O(10^7)$ ，但考虑到图8中瑞利数较大时数值模拟难以收束的情况，我们决定将同心圆区域内的瑞利数设置为 $Ra = 10^4$ 。此外，为了减少计算量，我们额外设置了一个边界条件，即在极坐标系 $(r, \theta)$ 下，方位角为 $\theta = 0^\circ$ 和 $\theta = 360^\circ$ 时的温度 $T$ 和流速 $\bm{v}$ 需要保持一致。

最终，我们获得了如图10所示的对流图像。从图10可以看出，瑞利数为10000时同心圆区域内会发生4个上升流和4个下降流，与现实世界中的地幔对流特征十分相似。

更加复杂的对流模拟——从矿物学的角度来看对流

在理论篇的末尾，我们从定性的角度介绍了相变对地幔对流的影响。那么，在考虑地幔内部相变的情况下，我们可以获得怎样的数值模拟结果呢？我们根据Christensen & Yuen (1985)的模型，在克拉佩龙斜率为 $\gamma = 0.3, 0.0, -0.3, -0.4, -0.6$ 时对矩形区域内的对流进行了数值模拟。其中，瑞利数被固定为 $Ra = 4\times 10^5$ 。最终，我们获得了如图11所示的对流图像。此外，为了更直观地呈现出相变对地幔对流的影响，因此我们在图11中也附上了描述物质处于何种相的图片。

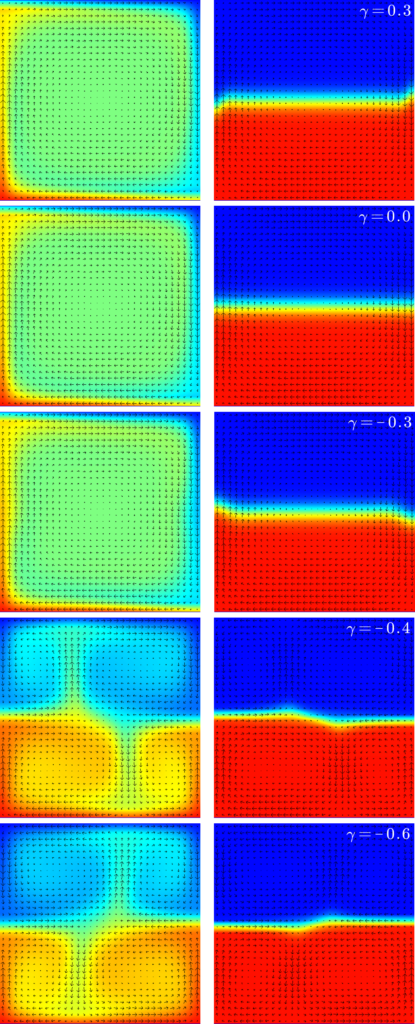
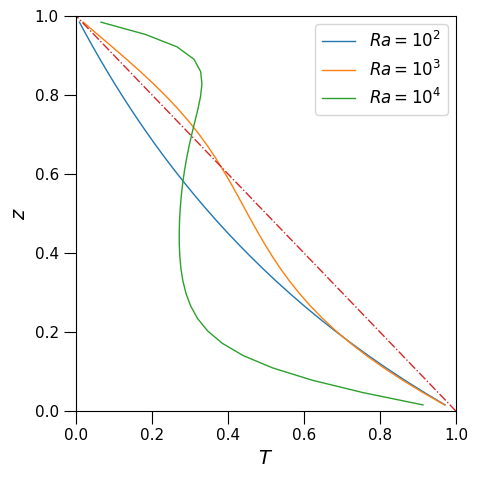
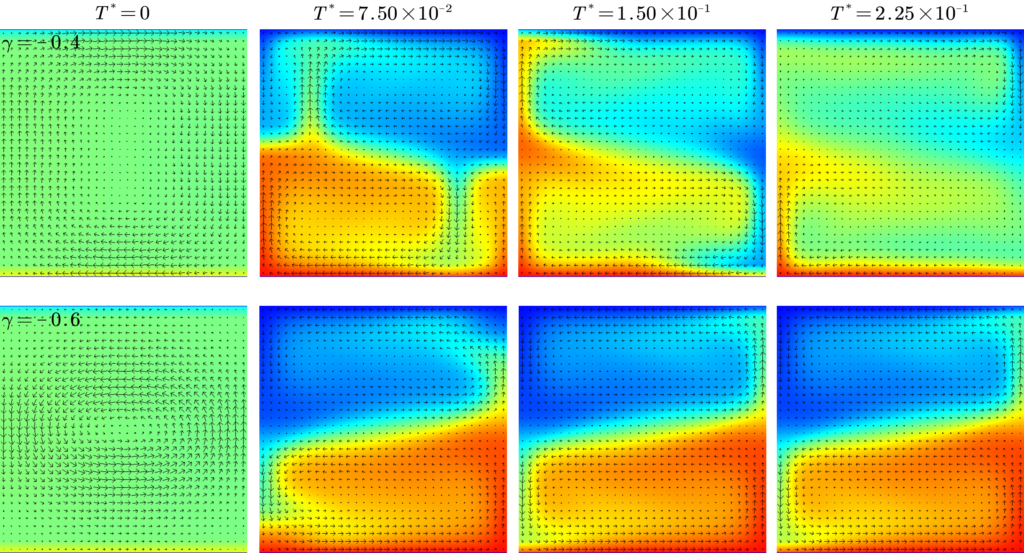
**图11** 不同克拉佩龙斜率下的矩形区域内的对流。其中，左侧图片展示了温度场和物质移速，右侧图片展示了物质处于何种相。需要注意的是， $\gamma \le 0.4$ 时的对流极不稳定，因此此处采用了无量纲化时间 $T^* = 2.50 \times 10^{-2}$ 时的计算结果。

在图11中，我们可以发现克拉佩龙斜率的绝对值较小（ $|\gamma| \le 0.3$ ）时，矩形区域内发生了较为稳定的单个对流循环。然而，在克拉佩龙斜率小于一定数值（ $\gamma \le -0.4$ ）时，矩形区域内被一分为二，发生了双层对流。特别值得注意的是，如图12所示，由于 $\gamma \le -0.4$ 时的对流极不稳定，因此我们未能获得稳定的对流图像。这可能是因为在相变发生时吸收的热量过多，相变界面附近的热量变化量过大，从而导致对流不易稳定。

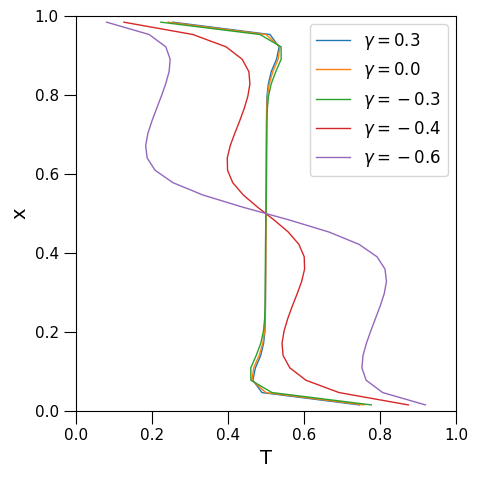
**图12** 克拉佩龙斜率为 $\gamma = -0.4, -0.6$ 时随时间变化的对流图像。可以发现对流难以稳定。

同样地，如果我们沿竖直方向计算平均温度分布，则可以获得如图13所示的图像。根据图13，我们可以得出克拉佩龙斜率越小，则越倾向于发生双层对流的结论。

如何再现出更加真实的对流？

看到这里的大家想必已经认识到了一个很严重的问题——以上的数值模拟都仅仅考虑了非常理想的情况下的对流，与地球内部实际发生的地幔对流可能有着很大的差别。

如果让我们短暂地头脑风暴一下，就可以想象出在地球内部有数不尽的物理量会影响到地幔对流的发生。例如，岩石的粘性率、物质的密度变化、物质的化学成分、地球自转产生的科里奥利力、局部的放射性元素放出的热量等。然而，精确地描述以上物理量是十分困难的。例如，正如式(10)所示，为了精确描述岩石的粘性率，我们需要知悉若干个物理量的具体值（Morishige & Honda, 2013）。甚至，如式(11)所示，由于在海洋板块俯冲至地幔内部时会携带大量的水，因此为了更加精确地描述岩石的粘性率，我们还需要考虑岩石的含水量（Dixon, et al., 2004）。

\begin{cases} \eta_\mathrm{diff} = A_\mathrm{diff} d^p \exp \left( \frac{E_\mathrm{diff}}{RT} \right) \\ \eta_\mathrm{disl} = A_\mathrm{disl} \tau^{1-n} \exp \left( \frac{E_\mathrm{disl}}{RT} \right) \\ \frac{1}{\eta} = \frac{1}{\eta_\mathrm{diff}} + \frac{1}{\eta_\mathrm{disl}} \end{cases} \tag{10}

\eta_\mathrm{eff} = \dot{\varepsilon}^\frac{1-n}{n} A^\frac{-1}{n} f_\mathrm{H_2 O}^\frac{-r}{n} \left\{ \exp \left( - \frac{PV + H}{RT} \right) \right\}^\frac{-1}{n} \tag{11}

为了模拟出更加真实的对流，世界各地的研究者们正夜以继日地优化模型和算法。然而，基于目前计算机硬件的性能限制，想要在短时间内对复杂模型进行计算是十分困难的。因此，我们还需要寄希望于计算机科学业界的专家们，希望他们能够早日在硬件开发上取得一个又一个的突破。此外，为了验证理论计算的结果的正确性，岩石实验乃至直接获取地幔物质样本也是十分重要的。综上所述，为加速地幔对流的数值模拟进展，让人类对地球内部发生的物理现象获得更为深入的理解，地球科学的各研究领域乃至计算机业界之间仍需加强沟通与融合。

参考文献

Blankenbach, B., Busse, F., Christensen, U., Cserepes, L., Gunkel, D., Hansen, U., … & Schnaubelt, T. (1989). A benchmark comparison for mantle convection codes. Geophysical Journal International, 98(1), 23-38.
Christensen, U. R., & Yuen, D. A. (1985). Layered convection induced by phase transitions. Journal of Geophysical Research: Solid Earth, 90(B12), 10291-10300.
Morishige, M., & Honda, S. (2013). Mantle flow and deformation of subducting slab at a plate junction. Earth and Planetary Science Letters, 365, 132-142.
Dixon, J. E., Dixon, T. H., Bell, D. R., & Malservisi, R. (2004). Lateral variation in upper mantle viscosity: role of water. Earth and Planetary Science Letters, 222(2), 451-467.