前言
为了向有意研究地球科学的青年学生提供接触前沿研究的机会,东京大学地震研究所于2024年3月举办了春之学校活动。作为日本乃至世界范围内规模最大的地震研究机构之一,在此次春校中,东京大学地震研究所共有10个研究室提供了五花八门的研究课题,涵盖了地震学、火山学、海啸工程学、计算机科学等领域。


作为一名有意利用高能物理学来解决地球科学问题的学生,最近我一直在关注地球中微子、地幔化学组成等问题。为了让自己对地球内部拥有更为清晰的认识、学习到更加前沿的研究手法,在此次春校中我选择了森重学(Morishige Manabu)先生策划的《地幔对流的数值模拟》课题。在3天的高强度交流中,我们基于流体力学的基础方程,参考了多种物理模型,利用数值模拟方法再现了地球内部的对流现象。
为了全面总结此次春之学校中学习到的内容,我决定将总结报告分为3篇进行更新(理论篇、实践篇、杂谈篇)。
地幔对流是什么?
我们人类赖以生存的地球其实并非一个完美的球体。如图3所示,地球内部可以被划分为多个不同的圈层。例如,根据组成物质的物理性质,我们可以将地球内部分为地壳、地幔、外核、内核这4个规模巨大的圈层。其中,除了由液体构成的外核外,地壳、地幔和内核都是由固体物质组成的。根据地球科学界的观测,液体的外核和固体的地幔之中都会发生对流现象。
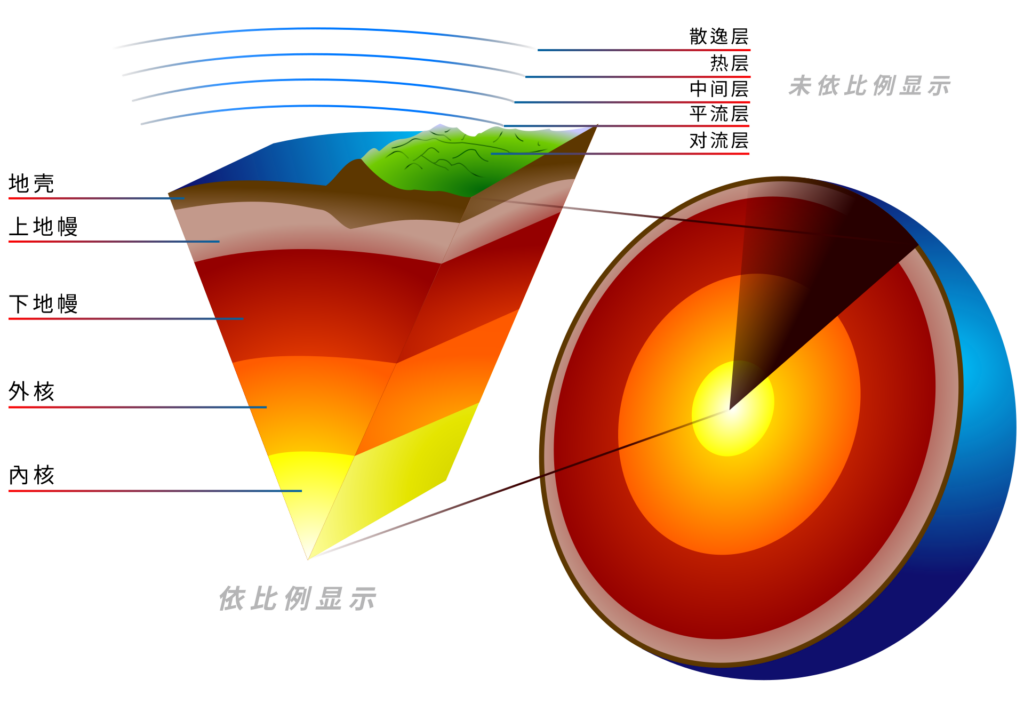
在此,或许有些人感到疑惑。在我们的认知中,正如味增汤一样,液体发生对流现象是十分常见的。然而,为什么固体的地幔也可以流动呢?地幔虽然是固体,但是在地球内部的高温和高压环境下,它仍然可以表现出类似流体的行为,这种流体行为被称为地幔对流(mantle convection)。地幔的高温高压环境使得其内部可以发生部分熔融,形成了称为岩浆(magma)的部分液态物质。此外,地幔内部的温度梯度也会导致物质的密度差异,从而产生密度梯度。这些密度差异和温度梯度共同作用,驱动了地幔内部的热对流。
那么,地幔对流从宏观上而言是什么样子的呢?如图4所示,从定性的观点来讲,地幔底部受到地核的热量影响而变热,从而导致地幔底部的岩石变得相对较轻,然后上升到地幔上部。同时,地幔上部冷却,岩石变得相对较重,然后下沉到地幔底部。这种上升和下沉的循环便构成了地幔对流。
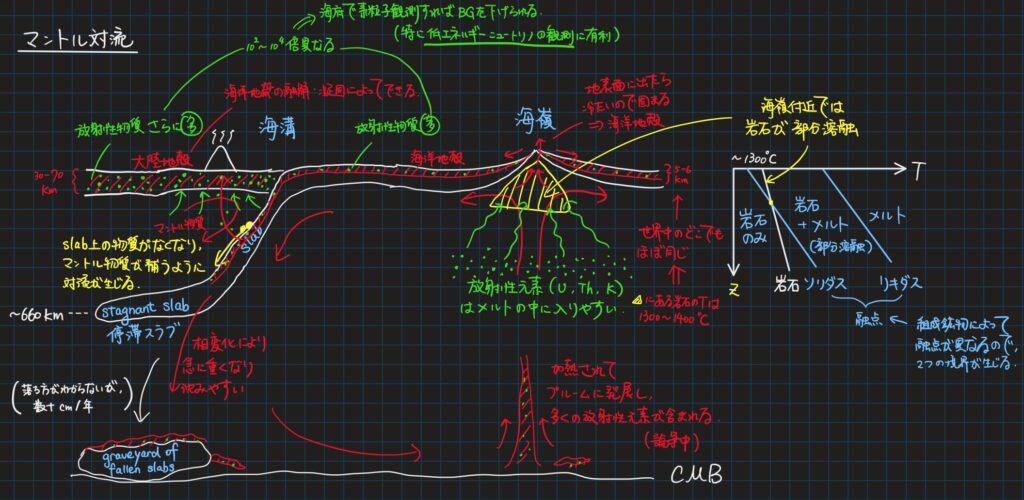
由于地幔对流现象在地球内部产生了大规模的热量输送,因此可以驱动地球板块的运动,从而影响地球表面的地质活动。如果追究根本,地震、火山喷发等现象的主要动力源便是地幔对流。因此,对地幔对流进行详细研究可以帮助人类进一步理解地震、火山喷发等灾害现象的起因。
地幔对流的基本方程式
学习过流体力学的同学都知道,如式(1)~(3)所示,我们可以根据质量守恒、动量守恒和能量守恒的微分方程来探究某一个区域内的流体的流动现象。需要注意的是,为了减少计算量,此处我们运用到了布辛涅司克近似(Boussinesq approximation),即将物质密度均看作是不随时间发生变化的常数。
\nabla \cdot \bm{v} = 0 \tag{1}-\nabla P + \nabla \cdot \{ \eta [ (\nabla \bm{v}) + (\nabla \bm{v})^\mathrm{T} ] \} + \rho_0 g \alpha T \bm{e}_z = 0 \tag{2} \frac{\partial T}{\partial t} + \bm{v} \cdot \nabla T = \kappa \nabla^2 T \tag{3}其中,式(1)~(3)中涉及到的符号所对应的物理量如表1所示。
表1 地幔对流的基本方程式中涉及到的物理量
| 符号 | 物理量 |
|---|---|
| \bm{v} | 对流速度 |
| P | 伴随对流产生的压强 |
| \eta | 介质的粘性率 |
| T | 介质的温度 |
| \bm{e}_z | 竖直方向上的单位向量 |
| t | 时间 |
| \alpha | 热膨胀系数 |
| \rho_0 | 介质的(基准)密度 |
| \kappa | 热扩散率 |
然而,由于上述式子中常数较多,并且常数之间的数量级差距也十分巨大,因此难以运用于数值计算之中。为了解决这些不便之处,在地球科学领域中常常会利用到无量纲化(nondimensionalization)的手法,即把上述方程中所有物理量的单位全部移除。此处,我们决定通过以下式子对各个参数进行无量纲化:
\left\{
\begin{array}{ll}
T = \Delta T T^* \\
\bm{v} = \frac{\kappa}{D}\bm{v}^* \\
\eta = \eta_0 \eta^* \\
P = \frac{\kappa \eta_0}{D^2} P^* \\
t = \frac{D^2}{\kappa} t^* \\
\bm{x} = D\bm{x}^*
\end{array}
\right. \tag{4}需要注意的是,在式(4)中,附有星号的参数均代表无量纲物理量。根据上述无量纲化,我们可以将式(1)~(3)改写为以下形式:
\nabla^* \cdot \bm{v}^* = 0 \tag{5}-\nabla^* P^* + \nabla^* \cdot \{ \eta^* [ (\nabla^* \bm{v}^*) + (\nabla^* \bm{v}^*)^\mathrm{T} ] \} + Ra T^* \bm{e}_z = 0 \tag{6} \frac{\partial T^*}{\partial t^*} + \bm{v}^* \cdot \nabla^* T^* = \nabla^{*2} T \tag{7}瑞利数
在式(6)中,出现了一个特别的无量纲数Ra。由于Ra在我们后续的数值模拟中起到十分重要的作用,因此我决定单独使用一个章节来介绍该无量纲数。这种无量纲数被称为瑞利数(Rayleigh number),具体定义为:
Ra = \frac{\rho_0 g \alpha \Delta T D^3}{\kappa \eta_0} \tag{8}其中, \Delta T 为特征温度, D 为空间的特征长度。
从定义上来讲,瑞利数是指通过自然对流传递的热量和热传导热量之比。也就是说,某个区域内的物质的瑞利数越大,则该区域内的热通过对流进行传递的比例越大;若某个区域内的物质的瑞利数越小,则该区域内的热通过热传导进行传递的比例越大。其中,热传导是指热根据热传导方程(式(9))进行传递的过程:
\frac{\partial u}{\partial t} = \kappa \nabla^2 u \tag{9}其中,\kappa为热扩散率。
那么,地幔的瑞利数大概是多少呢?我们可以利用表2中列出的值来粗略评估。
表2 概算地幔的瑞利数所需的物理量一览
| 物理量 | 值 |
|---|---|
| \rho_0 | 4 \times 10^3 \: \mathrm{kg/m^3} |
| g | 1 \times 10 \: \mathrm{m/s^2} |
| \alpha | 3 \times 10^{-5} \: \mathrm{K^{-1}} |
| \kappa | 1 \times 10^{-6} \: \mathrm{m^2/s} |
| \Delta T | 4 \times 10^3 \: \mathrm{K} |
| D | 3 \times 10^6 \: \mathrm{m} |
| \eta_0 | 1 \times 10^{22} \: \mathrm{Pa \cdot s} |
将表2中的值代入至式(8)中,我们可以概算出地幔的瑞利数的数量级为 O(10^7) 。由于瑞利数只要大于 O(10^3) 便可以发生对流,因此我们可以推测出地幔中可以发生规模极大的对流。
相变对地幔对流的影响
对热力学或者地球科学(特别是矿物学等领域)稍有深度了解的人都知道,几乎所有物质在不同的温度和压力下都会发生相变(phase transition)。相变是指某种物质在某个特定的温度和压力下,从一种相忽然变成另一种相的物理现象。在我们的日常生活中,最常见的相变便是冰变成水、水变成水蒸气之类的例子。
那么,地球内部会不会也可以发生相变现象呢?答案是肯定的。这是由于随着深度的增加,地球内部的温度和压力都会增加。在地幔和地核等较深的地方,由于温度和压力都足够高,使得岩石、金属等物质都会相变。这些相变现象对地球的内部结构和地球表面的地质活动都有重要影响。
在此,让我们从热力学的角度稍微深度展开一下。在热力学中,我们常用相图(phase diagram)来对某种物质的相变进行研究。为了定性说明相变对地幔对流的影响,我们决定使用横轴为温度 T ,纵轴为压强 P 的相图进行说明。在相图中,我们通常用直线或曲线来表示多个相的边界线。这种边界线的斜率 \gamma = dP/dT 被称为克拉佩龙斜率(Clapeyron slope)。当相变所对应的 \gamma > 0 时,我们称之为放热相变;若相变所对应的 \gamma < 0 时,我们称之为吸热相变。
如图5所示,若对放热相变进行定性分析,由于地幔柱的温度较通常的地幔物质高,因此地幔柱内的相变界面会向深处弯曲。相反,由于俯冲至地幔内部的海洋板块的温度较周边的地幔物质低,因此海洋板块内的相变界面会向浅处弯曲。最终,地幔柱会获得额外的浮力,而海洋板块会受到额外的重力。这种额外的力会促进地幔对流的发生。而吸热相变则与上述情况正好相反。
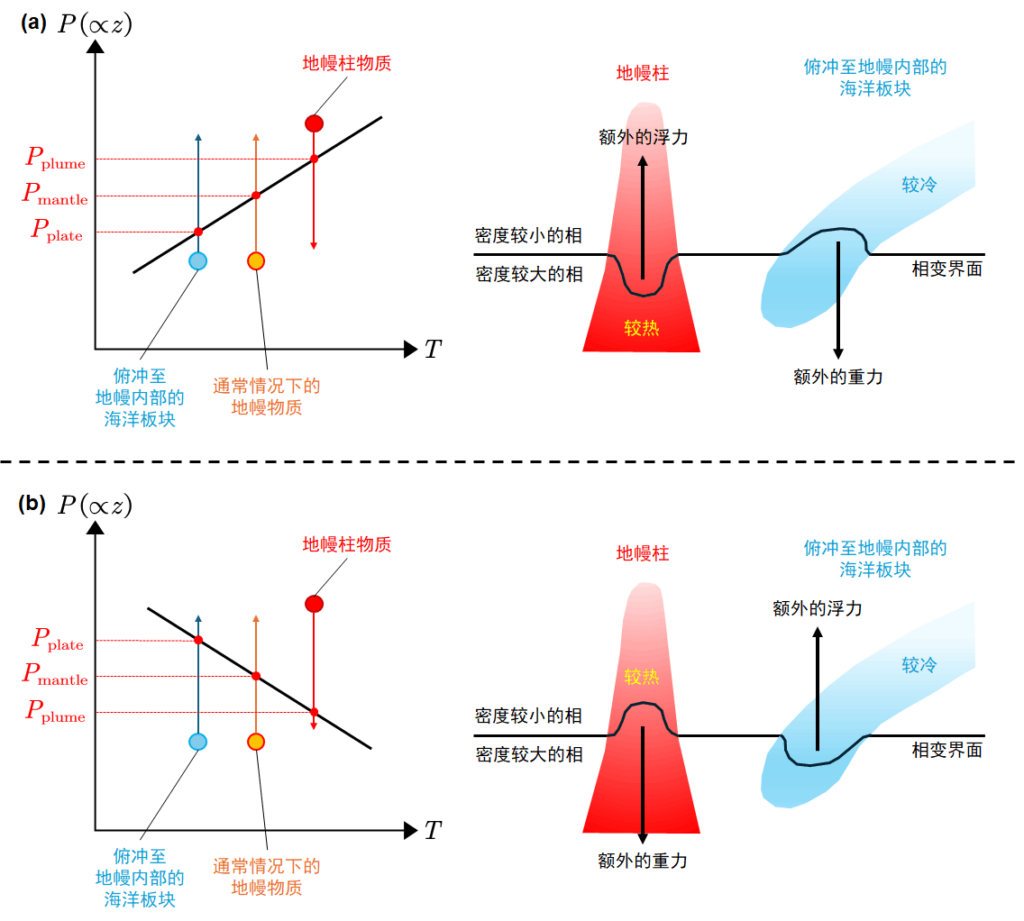
相信读完本章的你,一定对地幔中发生的相变产生了更深刻的理解。非常巧合的是,在“海亮杯”2022-2023学年全国中学生地球科学奥林匹克竞赛决赛(CESO2023决赛)中曾考过与地幔相变相关的题目(二、综合分析题中的Q10至Q12)。具有挑战心和好奇心的你不妨寻找原题(http://ceso.ssoc.org.cn/kejian/),来尝试解决一下相关问题。
那么,基于以上理论,我们可以通过数值模拟绘制出怎样的地幔对流图像呢?敬请参见实践篇。

3 comments