背景
最近我在上一门名为“地球物理观测解析学”的课程。该课程主要教授学生如何使用Python对地球物理观测结果进行分析。在探讨非线性最小二乘法时,老师按照惯例布置了一项Python作业。然而,这次的作业有点特殊——它涉及的数据集并非是地球物理学的观测数据,而是关于该课程学生提交作业数量(y)与距离提交截止的时间之间(x)的关系(图1)。
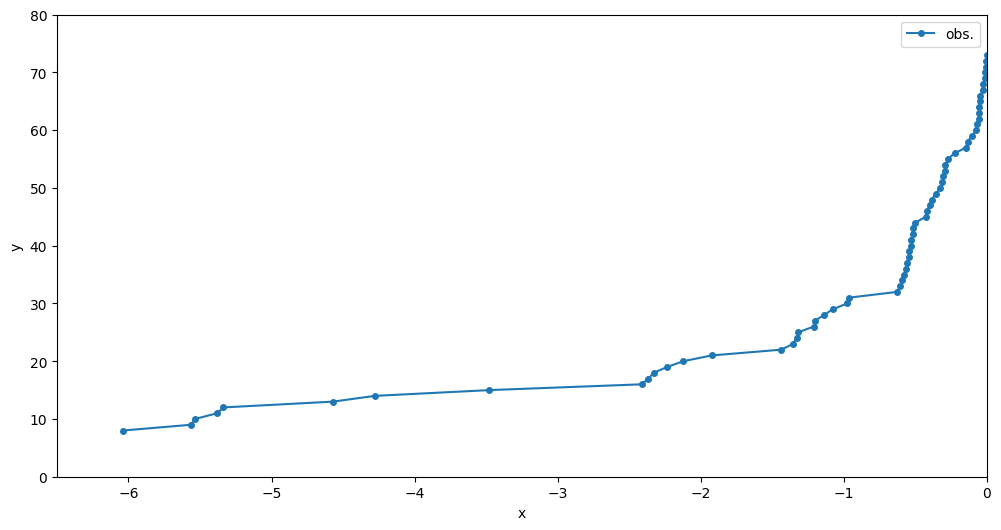
乍一看,只需要使用一个指数函数模型y(x) = A \exp{(\beta x)}就能轻松解决掉这次作业。然而,在不断试错后,我发现在这组数据集背后蕴含着一些更为深奥的秘密。
最初设想的几种模型
根据图1,很容易就能发现这次涉及到的观测量是随着时间单调递增的。因此,如表1所示,我引用了几个在计算机科学和物理学中经常用到的模型。不过,为了彰显出单调递增函数模型的适配性,我还特别增加了一个2次函数模型作为参考。
表1 最初设想的几种模型的参数和表达式
| 模型 | 参数 | 表达式 |
| 2次函数模型 | a, b, c | n(t)=at^2 + bt + c |
| 指数函数模型 | a, b, c | n(t) = a \exp(bt) + c |
| 逻辑斯蒂函数模型 | a, b, c, e | n(t) = \frac{a}{ 1+ \exp \{ -b(t-c) \}} + e |
| 双曲线函数模型 | a, b, c | n(t) = a \tanh(bt) + c |
最终,经过迭代10次的回归分析,我得出了如表3所示的回归结果。
表3 最初设想的几种模型的回归结果
| 模型 | 回归结果(迭代10次) | 残差 |
| 2次函数模型 | n(t)=3.90t^2 + 30.30t + 60.98 | 49.94 |
| 指数函数模型 | n(t) = 55.77 \exp(1.30t) + 13.03 | 19.80 |
| 逻辑斯蒂函数模型 | n(t) = \frac{86.97}{ 1+ \exp \{ -1.73(t+0.26) \}} + 11.64 | 32.55 |
| 双曲线函数模型 | n(t) = 52.92 \tanh(1.03t) + 67.65 | 23.92 |
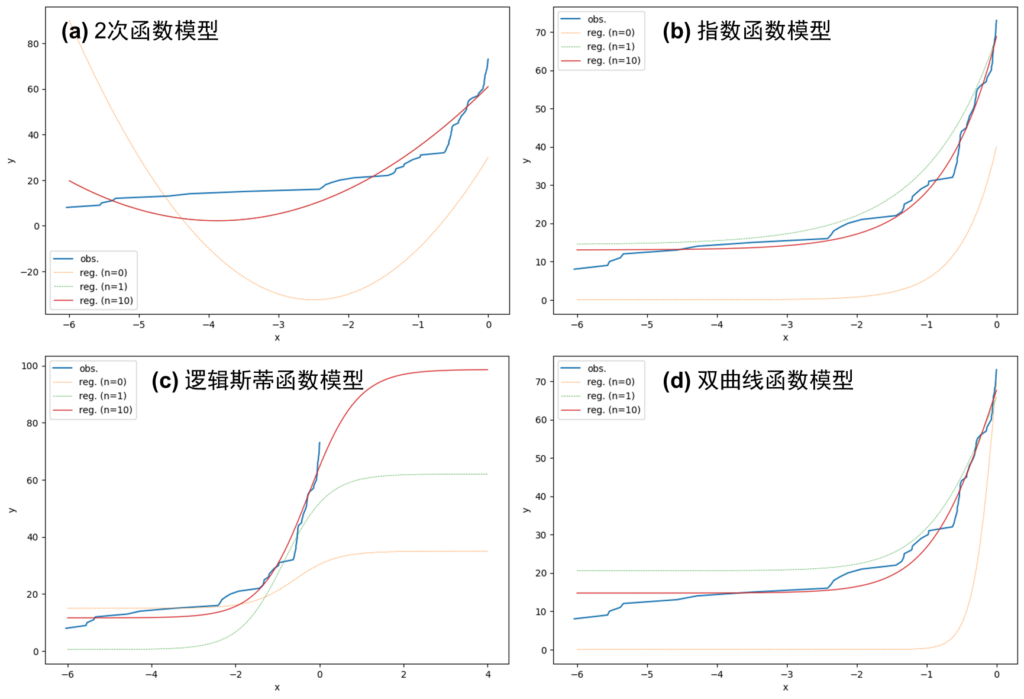
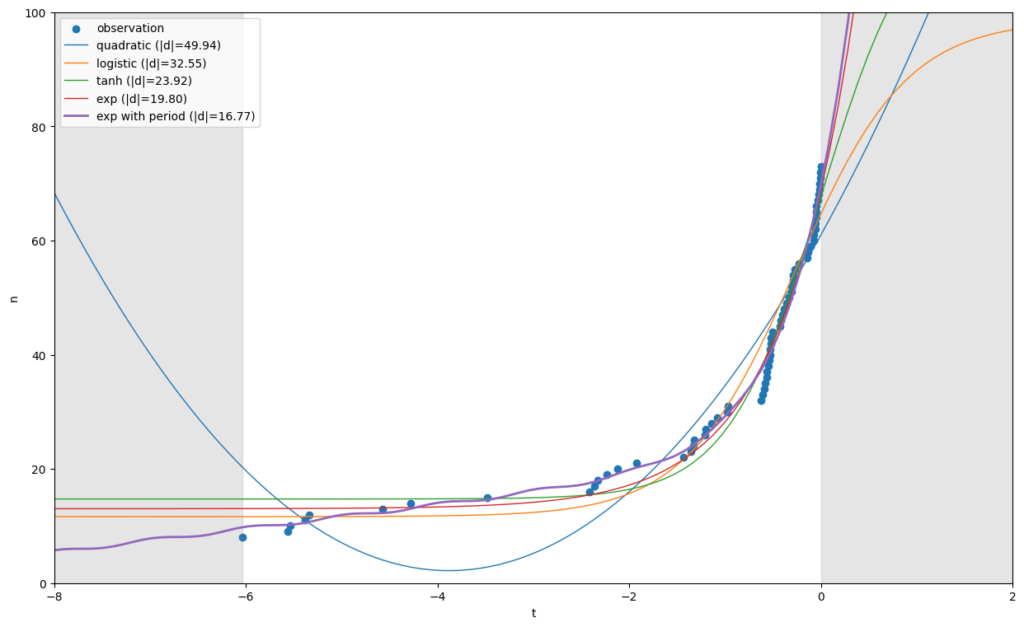
将这些回归结果与原始观测数据绘制成图表,便可得到图2。从图2可以看出,由于2次函数并非在定义域上一直呈现单调递增的性质,因此最终得到的回归结果与实际情况相差较大。而其他的3个模型由于都具有“先缓后急”、定义域上单调递增的性质,因此最终的回归结果基本与实际观测结果相吻合。
事实上,基本上所有同学在完成了上述回归分析后,便将结果总结成了PDF文档将作业提交了上去。然而,如果稍微思考一下,我们便能联想到一个极为重要的事实——通常情况下,绝大多数学生不太可能在凌晨、午休或者正常上课时间提交作业。对于这种情况的思考,让我觉得有必要继续深入展开探索。
考虑了1日周期的指数函数模型
如表1所示,由于指数函数模型和观测数据之间的残差范数||\bm{d}||最小,因此我决定在指数函数模型的基础上进一步展开调查。考虑到上一章末尾中提到的情况,我决定为指数函数模型只添加一个周期为1日的修正项。为了减少计算量,该修正项不考虑平日和周末的区别,也不考虑作业提交截止时间到来前为学生们施加的“紧张感”。
正如上文所说,由于观测量是随着时间单调递增的,因此周期修正项也应当具备这种性质。在考察了多种模型后,我决定在指数函数模型中添加如下的周期修正项。
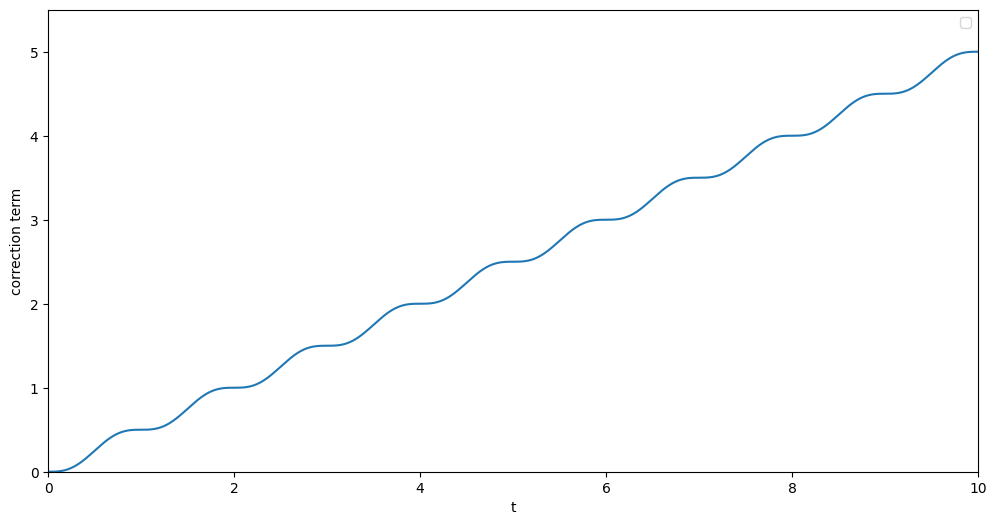
\Psi (t) \equiv\gamma \int_0^t \sin^2(\pi t' + \varphi) dt'
将周期修正项\Psi(t)进行绘图,我们便得到了如图3所示的函数图像。从图3可以看出,该周期修正项长得有点像是阶梯函数,确实具备单调递增、随1天周期发生变化等性质。
综上所述,考虑了1日周期的指数函数模型共有5个参数(\alpha, \beta, \gamma, \varphi, \delta),其表达式可写为
n(t) = \alpha \exp (\beta t) + \gamma \int_0^t \sin^2(\pi t' + \varphi) dt' + \delta
在该模型的基础上进行迭代10次的回归分析,我们得到了如下回归结果。
n(t) = 47.42\exp (1.66 t) + 4.13 \int_0^t \sin^2(\pi t' -0.88) dt' + 22.26
该回归曲线的残差仅有16.77,与一般的指数函数模型相比减少了15%左右。根据其初始相位\varphi = -0.88,我们还可以推测出在每天24时的\left| \frac{-0.88}{2\pi} \right| = 3.35小时前,即每天20时39分左右提交作业的人数是最多的。
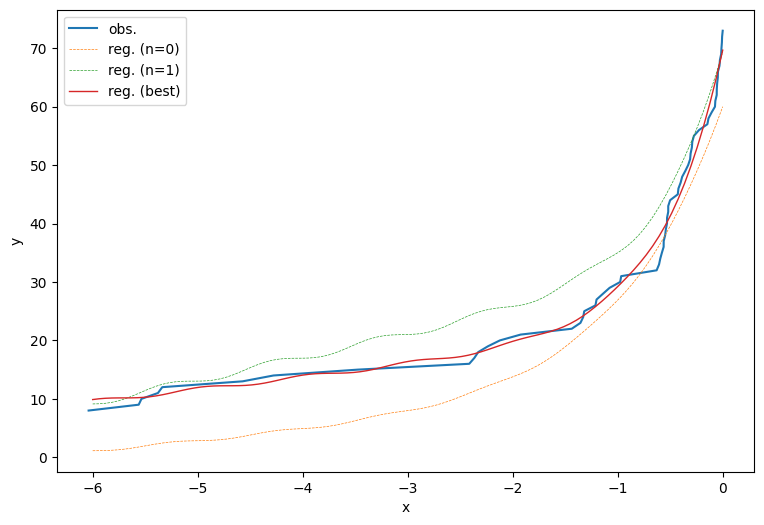
如图4所示,将回归曲线和观测结果绘制成图像,通过与图2中所示的4种模型进行比较,我们可以发现考虑了1日周期的指数函数模型更加贴合观测数据,并且在一定程度上展现出了周期变化。
总结
本文通过对“地球物理观测解析学”课程中作业提交量与距离提交截止的时间进行非线性回归分析,探讨了不同数学模型的适用性。结果表明,指数函数模型与实际情况最为相符。在该模型的基础上考虑周期为1日的修正项后,可以发现修正后的模型更加贴合观测数据,并且在一定程度上展现出了周期变化。
附:原理
[buy]以下内容适合对高等数学和回归分析等主题有一定了解的读者阅读。[/buy]
根据数据集的特点,我们可以将提交作业数n视为距离提交截止时间t的函数n(t)。由于该数据集共有66组数据,因此观测方程可写为
d_j = n_j^{\mathrm{obs}} - n_j \:(j = 1, 2, \dots, 66)将\alpha_i\:(i=1, 2, \dots, n)视为n(t)的参数,利用泰勒展开,可以得到如下的近似式。
n(\alpha_1 + \Delta \alpha_1, \alpha_2 + \Delta \alpha_2, \dots, \alpha_n + \Delta \alpha_n)
\cong n(\alpha_1, \alpha_2, \dots, \alpha_n)
+ \sum^n_{i=1} \frac{\partial n}{\partial \alpha_i}\Delta \alpha_i因此,关于正规方程式\bm{d} = \bm{y} - A\bm{x},则有
\bm{d} = \begin{pmatrix}
d_1 \\ \vdots \\ d_{66} \\\end{pmatrix}
\\
\bm{y} =
\begin{pmatrix}
n_1^{\mathrm{obs}} - n_1 \\ \vdots \\ n_{66}^{\mathrm{obs}} - n_{66} \\\end{pmatrix}
\\
A =
\begin{pmatrix}
\frac{\partial n}{\partial \alpha_1}|_{t=t_1} &
\frac{\partial n}{\partial \alpha_2}|_{t=t_1} & \dots &
\frac{\partial n}{\partial \alpha_n}|_{t=t_1} \\
\frac{\partial n}{\partial \alpha_1}|_{t=t_2} &
\frac{\partial n}{\partial \alpha_2}|_{t=t_2} & \dots &
\frac{\partial n}{\partial \alpha_n}|_{t=t_2} \\
\vdots & \vdots & \vdots & \vdots \\
\frac{\partial n}{\partial \alpha_1}|_{t=t_{66}} &
\frac{\partial n}{\partial \alpha_2}|_{t=t_{66}} & \dots &
\frac{\partial n}{\partial \alpha_n}|_{t=t_{66}} \\\end{pmatrix}
\\
\bm{x} = \begin{pmatrix}
\Delta \alpha_1 \\ \Delta \alpha_2 \\ \vdots \\ \Delta \alpha_n \\\end{pmatrix}通过将残差向量\bm{d}的欧几里德范数(L2范数)||\bm{d}||^2最小化,可以求出参数的变化量\bm{x}为
\bm{x} = (A^T A)^{-1} A^T \bm{y}通过\alpha_i \rightarrow \alpha_i + \Delta \alpha_i对参数进行更新,重复上述步骤10次,便可大致求出精度较好的回归曲线系数。