基于热量收支方程和整体法的地表温度近似式
T_s \cong \frac{R - \sigma T^4 - l\rho \beta g_a q_{SAT}(T)(1-h)}
{4\sigma T^3 + c_p \rho g_a + l\rho \beta g_a \Delta(T)} + T \tag{*}其中,式(*)中出现的各个记号所对应的物理量如下表所示。
| 物理量 | 记号 | 单位 |
| 地表温度 | T_s | \rm{K} |
| 气温 | T | \rm{K} |
| 斯忒藩-玻尔兹曼常数 | \sigma | \rm{W \: m^{-2} \: K^{-4}} |
| 净辐射通量(*) | R=(1-A)S_\downarrow + L_\downarrow | \rm{W\: m^{-2}} |
| 水的汽化潜热 | l | \rm{J \: kg^{-1}} |
| 质量密度 | \rho | \rm{kg\: m^{-3}} |
| 地表的蒸发效率 | \beta | \rm{1} |
| 显热交换效率 | g_a | \rm{m\: s^{-1}} |
| 饱和比湿 | q_{SAT} | \rm{kg\:kg^{-1}} |
| 比湿 | h | \rm{kg\:kg^{-1}} |
| 饱和比湿的温度变化率 | ∆(T) = dq_{SAT}(T)/dT | \rm{kg\:kg^{-1}\: s^{-1}} |
(*)净辐射通量R:指太阳辐射通量S_\downarrow、地表反射率为A时的反射辐射通量A S_\downarrow以及长波辐射通量L_\downarrow的总和。此处的长波辐射通量不包含地面辐射通量\sigma T_s^4。
近藤(1992)认为,理解地表温度,除了对于解决农业气象问题和城市变暖问题之外,对于从卫星观测中了解热收支、水收支的课题来说也是十分重要的。然而,在现实中,我们很难直接获取关于地表温度的信息——想必大家都没有听说过直接设置在地表的气象仪吧!因此,我们需要寻找一种可以利用距离地表数米的气象数据来推测地表温度的方法。而式(*)便是其中之一。
式(*)的推导
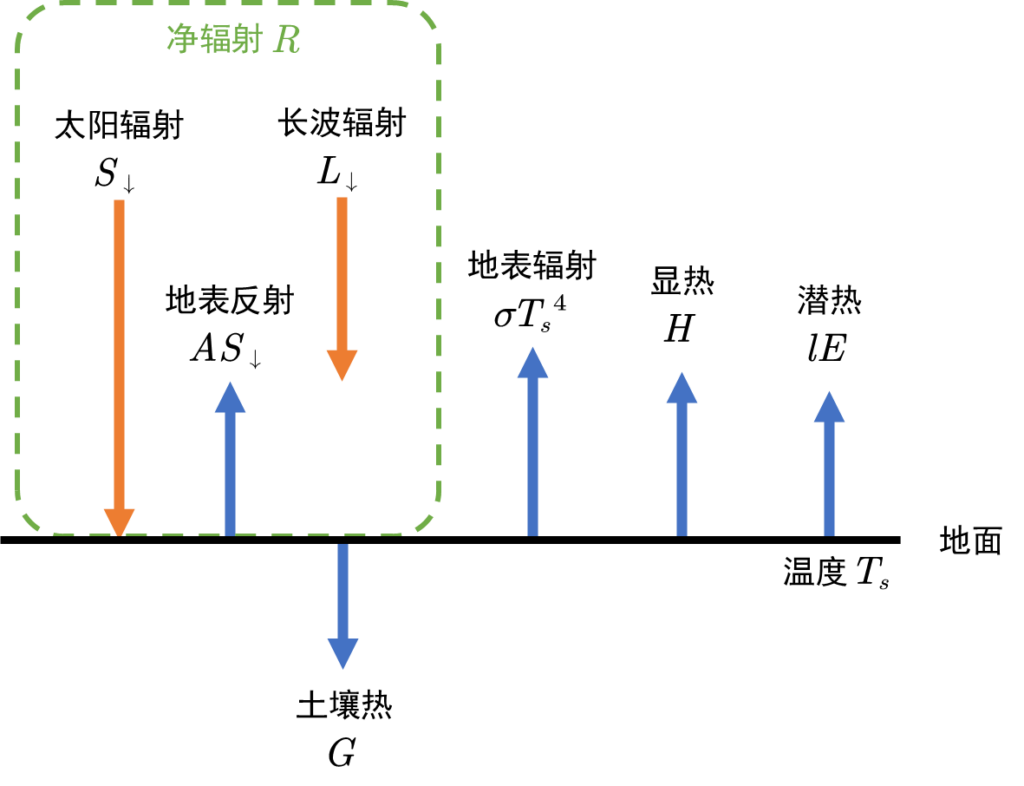
如下图所示,若将太阳辐射通量设为R、显热通量设为H、潜热通量设为lE、土壤热通量设为G,则地表的热量收支方程可表示为
R - σT^4_s = H + lE + G \tag{1}其中,\sigma是斯忒藩-玻尔兹曼常数,T_s为地表温度。
将σT^4_s进行关于温度T的一阶泰勒展开,则有
σT^4_s \cong σT^4 + 4σT^3(T_s - T) \tag{2}再将潜热通量lE的整体法表达式进行关于温度T的一阶泰勒展开,则有
lE = lρβg_a(q_{SAT}(T_s) - q) \cong lρβg_a{q_{SAT}(T) + ∆(T)(T_s - T) - q} \tag{3}其中,∆(T) = dq_{SAT}(T)/dT。
将显热通量的整体法表达式
H = c_pρg_a(T_s - T) \tag{4}以及式(2)(3)一同代入至式(1),并且无视土壤热通量G的影响,则可以得到如下近似式。
R - σT^4 - 4σT^3(T_s - T) \cong c_pρg_a(T_s - T) + lρβg_a{q_{SAT}(T) + ∆(T)(T_s - T) - q} \tag{5}此时,将相对湿度h \equiv q/q_{SAT}(T)这一概念导入后对式(5)进行整理,则可以得到
R - \sigma T^4
- l\rho \beta g_a q_{SAT}(T) \left( 1-\frac{q}{q_{SAT}(T)} \right)
\cong \{ 4\sigma T^3 + c_p \rho g_a + l\rho \beta g_a \Delta(T) \}(T_s - T)
\tag{6}对式(6)进行整理,便可以得到如下的地表温度近似式了。
T_s \cong \frac{R - \sigma T^4 - l\rho \beta g_a q_{SAT}(T)(1-h)}
{4\sigma T^3 + c_p \rho g_a + l\rho \beta g_a \Delta(T)} + T \tag{*}参考文献
- 近藤純正. (1992). 地表面温度と熱収支の周期解及びその応用. 農業気象, 48(3), 265-275. https://doi.org/10.2480/agrmet.48.265.(日语)