什么是中微子?
正如我在《论文笔记:Partial radiogenic heat model for Earth revealed by geoneutrino measurements》一文中讲到,中微子(neutrino)是目前人类已知的亚原子粒子中最轻的粒子。由于它不具有可被测量的电磁特性,并且在忽略重力的情况下仅通过弱核力相互作用,因此中微子可以以接近光速的速度畅通无阻地穿过各种物质。
那么,中微子起源于哪里呢?根据物理学界长期以来的研究,人们早已发现中微子可通过放射性衰变、核反应等多种方式产生。或许大家听到“中微子”一词感到十分陌生,但其实在我们的日常生活中存在着很多巨大的天然中微子源。例如,由于在太阳内部时时刻刻都在发生着4 \mathrm{^{1}_{1} H} + 2 e^- \rightarrow \mathrm{^{4}_{2} He} + 2\nu_e的核反应,因此太阳无时无刻都在释放着大量中微子。根据Bahcall等人(2005)的推算,在每一秒钟之内,地球表面每平方厘米上平均会穿过大约650亿个来自太阳的中微子。
作为对地球科学也十分感兴趣的我,不妨也在此向读者介绍一种出乎很多人意料的中微子来源。在我们人类生存的地球内部其实也蕴含着大量诸如238-U、235-U、232-Th、40-K等放射性同位素。通过观测不断产生自这些放射性同位素的中微子,可以帮助人类对地球内部的化学组成、热源分布等有更清晰的认识。这种来源于地球内部的中微子也被称为地球中微子(geoneutrino)。地球中微子早在上世纪60年代中期就被预测存在了,但直至2005年才被日本东北大学中微子科学研究中心(Research Center for Neutrino Science, Tohoku University)在岐阜县神冈矿山设置的KamLAND首次观测到(Araki等人,2005)。
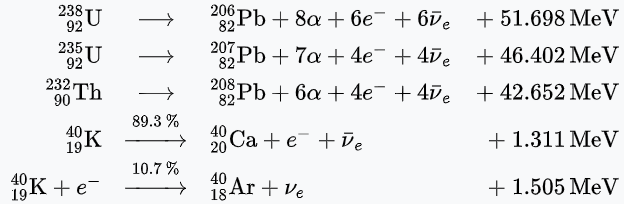
顽皮的中微子——中微子振荡现象
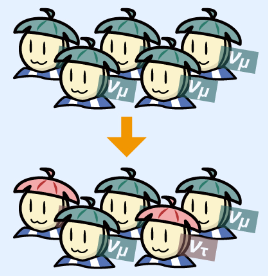
说起中微子最出名的现象,就不得不提到中微子震荡现象(neutrino oscillation)了。对粒子物理学等稍有了解的朋友们都知道,在基本粒子标准模型中,中微子同其他轻子一样,被分为了“电中微子(\nu_e)”、“μ中微子(\nu_\mu)”和“τ中微子(\nu_\tau)”3个世代(generation)。而中微子在空间中传播时,会根据某种特定周期转化成不同的世代。这种现象便被物理学家们称为中微子震荡现象。
不过,人们至今也未能够完全理解中微子振荡现象。为了让读者们认识到中微子震荡是一种多么复杂的现象,我决定在此处加入一些稍微深入的物理学知识。如果将参与弱相互作用的中微子场数式化,根据日本物理学家牧二郎、中川昌美和坂田昌一的理论,则可以表示为\ket{\nu_\alpha (t)} = \sum_j U^*_{\alpha j} \ket{\nu_j (t)} (\alpha = e, \mu, \tau; j = 1, 2, 3)。其中,矩阵U为
U = \begin{pmatrix}
U_{e1} & U_{e2} & U_{e3} \\
U_{\mu1} & U_{\mu2} & U_{\mu3} \\
U_{\tau1} & U_{\tau2} & U_{\tau3} \\
\end{pmatrix}
= \begin{pmatrix}
\cos \theta_{12} \cos \theta_{13} & \sin \theta_{12} \cos \theta_{13} & \sin \theta_{13} e^{-i \delta} \\
-\sin \theta_{12} \cos \theta_{23} - \cos \theta_{12} \sin \theta_{23} \sin \theta_{13} e^{i\delta} & \cos \theta_{12} \cos \theta_{23} - \sin \theta_{12} \sin \theta_{23} \sin \theta_{13} e^{i\delta} & \sin \theta_{23} \cos\theta_{13} \\
\sin \theta_{12} \sin\theta_{23} - \cos \theta_{12} \cos \theta_{23} \sin \theta_{13} e^{i \delta} & -\cos\theta_{12} \sin\theta_{23} - \sin \theta_{12} \cos \theta_{23} \sin \theta_{13} e^{i \delta} & \cos \theta_{23} \cos \theta_{13} \\
\end{pmatrix}为了同时纪念成功预测了中微子震荡现象的苏联物理学家布鲁诺·庞蒂科夫,该矩阵也被称为庞蒂科夫-牧-中川-坂田矩阵(Pontecorvo-Maki-Nakagawa-Sakata Matrix,简称PMNS矩阵)。
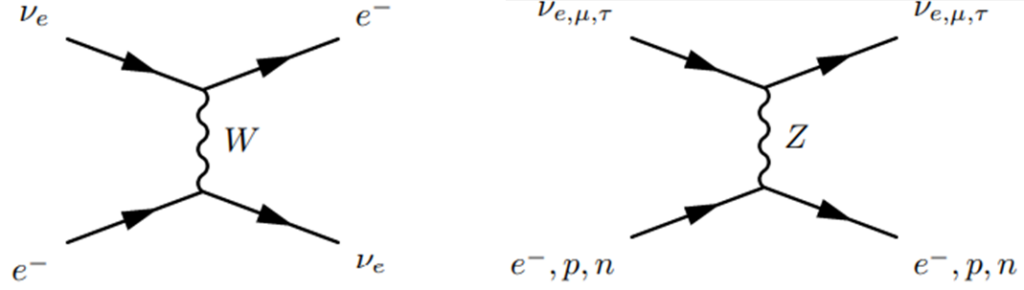
此外,与在真空中的情况相比,在物质中的中微子震荡现象更为特殊。这是因为在物质中,中微子可以通过弱核力(W及Z玻色子)与物质中的电子、质子、中子相互作用,从而获得额外的势能V(x) \propto n_e(x)。因此,中微子振动的周期将会有所改变。
为什么中微子振荡在理论上可以用来预测地震?
Wang等人(2011)认为,基于中微子振荡现象,通过观测中微子生存概率的异常可以对地震进行预测。
具体而言,Wang等人(2011)认为可以将核电站等中微子源释放出的中微子作为“探针”。为了获取这些“探针”收集到的信息,我们需要将中微子源和需要做出地震预测的区域连成直线,并在直线与地球表面的另一交点处设置中微子探测器。Wang等人(2011)引用了Namgaladze等人(2009)的观点,即在地震发生前,震源域会出现起源于物质密度异常的电子密度异常。正如上一章中介绍的一样,由于物质中电子密度的差异可以使得中微子振荡的结果略微出现不同,因此这种电子密度异常可通过观测中微子的世代变化(即中微子生存概率的异常。其中,中微子生存概率是指某个初始世代的中微子在传播过程中保持其原始世代的概率)来推测。
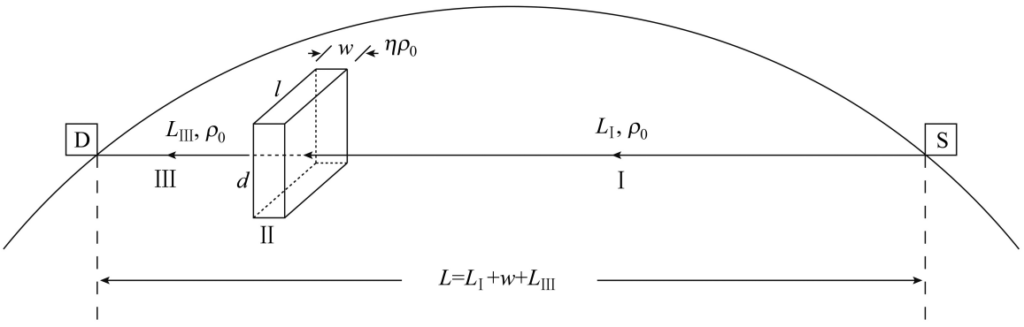
为了量化Namgaladze等人(2009)提出的发生于震前的电子密度异常现象,Wang等人(2011)假设在地震发生前,组成断裂带的物质的平均密度与该区域的总电子密度成正比,并假设震前的平均物质密度为平稳期的η倍。在η=3时,若将观测基线设为从龙门山断裂带到大亚湾核反应堆之间的长达1418 km的线段,则理论上在基线延伸到另一端地表的观测点处可观测到能量较小的中微子的生存概率异常。其中,断层的尺寸越大,中微子生存概率异常的相对比例就越大,最多可以达到3%。这也意味着,对于规模越大的地震,利用该方法预测成功的可能性就越大。
这种理论可行吗?
“理想很丰满,现实很骨感”。上述理论乍一看似乎很有可行性,但其实基于目前的技术而言,通过该理论来对大地震进行预测是不现实的。例如,阻拦该理论实践运用的一大障碍便是PMNS矩阵中的仍有一些参数未能被准确测量。
此外,研究组还提到,只有商用核反应堆释出的中微子才适用本文提到的理论,而加速器设施生成的中微子无法适用本文的方法。这是因为前者的能量仅为MeV级,而后者高达数GeV。由于中微子的能量越大,则观测所需的基线长度就越大,因此若想要得观测到GeV级的中微子生存概率异常,在人类可以大规模开发太空资源前,这对于半径仅为约6400 km的地球而言难以实现。
还需要强调的是,在现实生活中,有许多诸如地球中微子、太阳中微子等核反应堆外的中微子源,这将导致观测“探针”中微子变得十分不易。此外,基于世界各地普遍缺乏中微子观测设施的现状,用于观测中微子的设施的数量、精度和稳定性都需要得到大幅度的提升。更为重要的是,本文的假设基础——震前的电子密度异常现象是否如实还有待证实。即便该现象被证实存在,其与平稳期的电子密度之间的关系也有待考察。
写在最后
近年来,随着学科之间的互相交融,面对地震预测这一地震学界苦战百余年也未能解决的终极难题,有诸多其他领域的学者纷纷加入到了解决难题的行列中。例如,随着近十年的计算机发展狂潮,在计算机科学领域中诞生出了试图对地震进行预测的机器学习模型(详情请见《真假难辨——来自巴基斯坦的地震预测研究》)。而本文中,Wang等人(2011)从粒子物理学的角度出发,大胆提出了新颖的理论设想,这无疑将对未来的地震学的相关研究产生更多新鲜的刺激。希望人类可以在不久的将来,能够克服一系列难题,最终征服地震预测这一巨大的挑战。
参考文献
- Wang, B., Chen, Y. Z., & Li, X. Q. (2011). Earthquake forecast via neutrino tomography. Chinese Physics C, 35(4), 325-332.
- Bahcall, J. N., Serenelli, A. M., & Basu, S. (2005). New solar opacities, abundances, helioseismology, and neutrino fluxes. The Astrophysical Journal, 621(1), L85.
- Araki, T., Enomoto, S., Furuno, K., Gando, Y., Ichimura, K., Ikeda, H., … & Piquemal, F. (2005). Experimental investigation of geologically produced antineutrinos with KamLAND. Nature, 436(7050), 499-503.
- Namgaladze, A. A., Klimenko, M. V., Klimenko, V. V., & Zakharenkova, I. E. (2009). Physical mechanism and mathematical modeling of earthquake ionospheric precursors registered in total electron content. Geomagnetism and Aeronomy, 49, 252-262.