本文为《一种解决Minecraft服务器常见经济问题的新尝试》专题的第2篇文章。上文请见背景篇。
注意:本文将出现大量数学公式,可能需要高等数学等知识储备。
大蛋糕不如小蛋糕——专属于每位玩家的额度池
我想,既然在第2代收购系统中,玩家因为“秒空”现象屡屡发生而无法为自己抢到额度,直接为每位玩家分配一定数量的额度或许是最好的办法。考虑到玩家获取的DC币(DC服务器里使用的货币)总数应当与其在服务器内的活跃程度挂钩,单个玩家的收购额度Q可以根据下述公式决定:
Q \propto (Q_{B}+\gamma P)T其中,T为收购总额度,Q_{B}为保底收购额度,P为活跃时长总数,\gamma为常数。通过该式子,占据Minecraft服务器多数的学生玩家可在不需要频繁上线的情况下就能获得一定收购额度,从而保障学生玩家专注于学业,达到“劳逸结合”的目的。
从现实汲取灵感 避免重蹈覆辙——价格浮动制
此外,为了避免第1代收购系统中扎堆挖矿、无暇理会其他玩法等不健康现象的出现,我决定仿照现实世界引入商品价格浮动制。在不断试错后,我发现可以通过基于单个玩家的售出某物品的历史总量来计算该玩家的单个物品的收购价格。
具体而言,我们希望单个物品的收购价格p(n)应随着单个玩家的历史售出总量n的增多而逐渐减少,但该玩家通过该物品赚到的货币量M(n) = \sum_{n'=0}^n p(n')应为单调递增的凹函数。对此,M(n)可设为形同M(n) \propto \ln n的函数。然而,在这样的假设下,单个物品的收购价格必须满足p(n) \propto^{-1} n。这意味着我们难以通过引入其他系数的方式来对价格的衰减率进行调整。为解决该问题,我们试图通过指数函数的补函数来定义M(n),即
M(n) \propto 1 - e^{-\lambda n}其中,\lambda为衰减系数。此时,为方便计算,假设M(n)满足
M(n) = \int_0^n p(n') dn' = \frac{1}{\lambda} ( 1- e^{-\lambda n} )则可以求得单个物品的收购价格为
p(n) = e^{-\lambda n}通过该式子的定义,我们便可以轻松对单个物品的收购价格的衰减规律进行控制了。
我们还可以根据上述式子,依据环境因素,对单个玩家的单个物品的收购价格p(n)进行扩充定义:
p(n, t) = \varepsilon(t) \iota(t) p_0 e^{-\lambda n}其中,\varepsilon(t)为经济环境指数,\iota(t)为特别物价指数,p_0为该物品的原始收购价格,n为该玩家的该物品的历史售出总量,\lambda为价格衰减系数。
此外,为防止因历史售出总量n过大导致单个玩家的单个物品的收购价格p(n)长期处于较低的水平,n应当随着现实时间t缓慢减小,从而使得物品收购单价p(n)可以随着现实时间t缓慢恢复至原本的水平。我们通过考察一系列符合条件的函数,最终选定n \equiv n(t)为
n(t) = \frac{n(0)}{e^{\delta(t-\tau)} + 1}其中,t为售出该物品起算的时间,\delta为逆时间系数,\tau为时间系数。该式子即为在经济学、社会学、生物学、地球科学等领域中被频繁使用的逻辑斯谛函数。这种函数在起始阶段时大致显示出指数增长的趋势,但随时间发展变得逐渐饱和,增长变慢。最后,进入成熟阶段时增长率将基本接近于0,增长停止。
然而,需要注意的是,玩家在不同时期出售的物品需要分别适用于上述式子。因此,在计算单个玩家的单个物品的收购价格时,还必须考虑该物品在不同时期的出售历史。此外,由于n(t)应当是一个非负的整数,因此需要对每个周期对应的n(t)进行下取整。综上所述,上述式子需要改写为
n(t) = \sum_{i=1}^\infty \left\lfloor {\frac{n(0)}{e^{\delta(t-\tau)} + 1}} \right\rfloor其中,对于i=1,2,…,n_i(t_i)代表在第t_i周期内出售的相应物品的数量。
在实践中,为了节省数据的存储量,对历史上所有的出售行为都进行记录是不可取的。对此,假如我们设置某个物品在一个周期内的出售数量上限为\nu,则我们可以将需要记录的时间最大值设为
T = \inf{t} \:\:\: \mathrm{s.t.} \:\:\: \left\lfloor {\frac{\nu}{e^{\delta(t-\tau)} + 1}} \right\rfloor = 0考虑到上述式子和DC币的最小单位为1分(0.01 DC币)的事实,可得单个玩家的单个物品的收购价格为
p(n) = \mathrm{round} \left\{ \varepsilon(t) \iota(t) p_0
\exp \left( -\lambda \sum_{i=1}^T \left\lfloor {\frac{n_i(0)}{e^{\delta(t-\tau)} + 1}} \right\rfloor \right), 2 \right\}其中,\mathrm{round} \{x, n\}为将x四舍五入,保留至小数点后n位的函数。
偶尔为玩家们带来小惊喜——经济环境指数与特别物价指数
在上文中,我们引入了经济环境指数\varepsilon(t)与特别物价指数\iota(t)。这两个指数的引入旨在使物价能够根据当前周期内服务器的活跃程度、玩家参与收购的程度以及玩家集中出售物品的种类进行波动。
关于经济环境指数\varepsilon(t),我们将其定义为
\varepsilon(t) = \left\{ 1 - \sum_{i \in \text{中长假期}} \alpha_i
\exp \left[ {-\frac{(t - \mu_i)^6}{2\sigma_i^2}} \right] \right\} \times \beta(t)
+ n(t)其中,中长假期指寒假、暑假、国庆假期,\mu_i为每个中长假期的时间中值,\alpha_i, \sigma_i为与每个中长假期相关的常数:
\alpha_i = \begin{cases}
0.15, & i \in \{\text{寒假}, \text{暑假}\} \\
0.075, & i = \text{国庆假期}
\end{cases}, \quad
\sqrt[4]{\sigma_i} = \begin{cases}
16, & i \in \{\text{寒假}, \text{暑假}\} \\
2.4, & i = \text{国庆假期}
\end{cases}n(t)为Gauss噪声:
n(t) \sim \mathcal{N}(0, \sigma_n^2)
= \frac{1}{\sqrt{2\pi}\sigma_n} \exp\left(-\frac{x^2}{2\sigma_n^2}\right)
\quad \mathrm{where} \quad \sigma_n=0.025\beta(t)为反映周末及清明、劳动节、中秋节等小假期时的物价系数:
\beta(t) = \begin{cases}
0.95, & t \in \text{小假期} \\
0.98, & t \in \text{中小假期以外的周末} \\
1, & \text{其他情况}
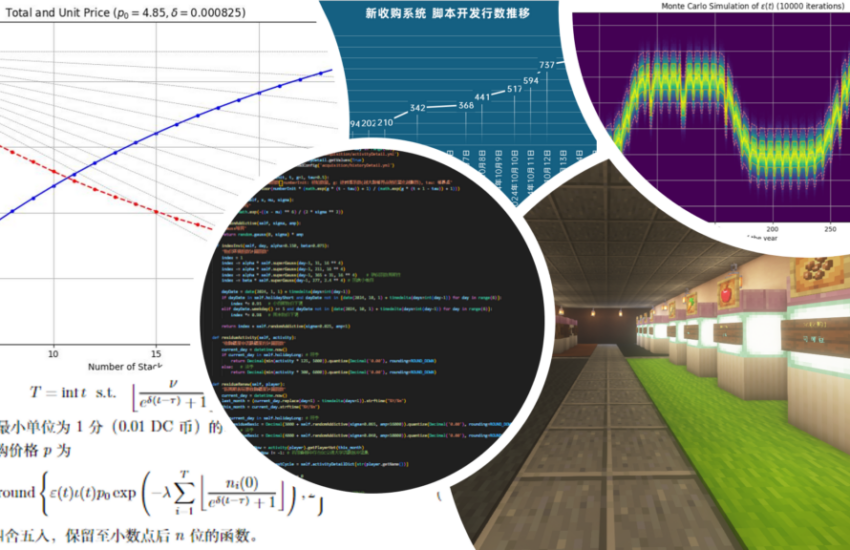
\end{cases}图4展示了物价环境指数\varepsilon(t)在某年全年内通过10000次Monte Carlo模拟后的分布结果。横轴表示一年中的具体日期,纵轴表示模拟得到的物价环境指数值。二维频度图的颜色从浅到深表示不同的模拟频率,浅色区域表明在该日期范围内,\varepsilon(t)更有可能出现在这些取值范围内。可以观察到,在寒假、暑假和国庆这三个中长假期,经济环境指数大幅下降;而在非长假期间的淡季,经济环境指数则恢复到接近1的正常水平。此外,根据校正,周末和小假期时的经济环境指数也有所下降,但下降幅度相对较小。通过加入Gauss噪声n(t),可以为玩家们带来因物价浮动而来的惊喜。物价环境指数虽然变得不可预测,但是整体趋势与冷淡季应有的经济水平相符。因此,我们认为物价环境指数以上述式子的形式表达是符合科学规律的。
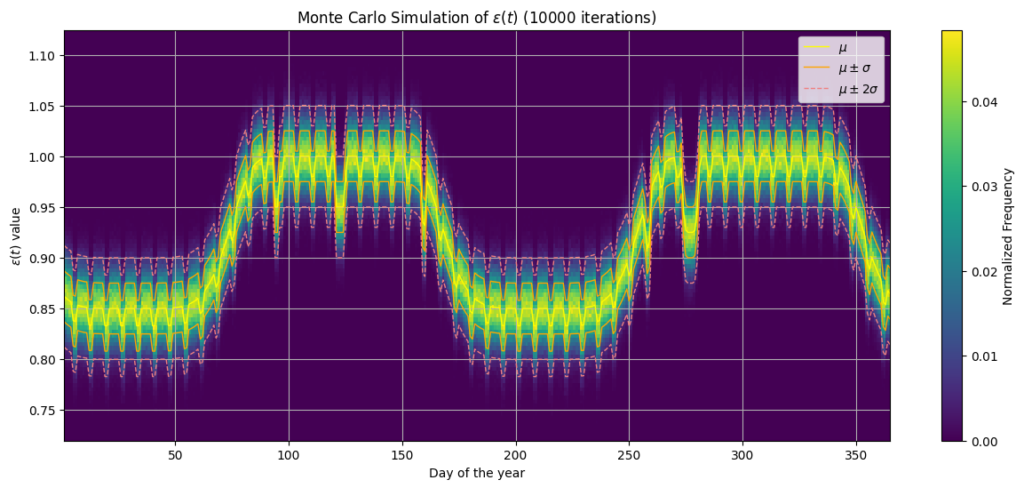
对于特别物价指数\iota(t),我们则采用人工赋值的方式。例如,通过不定期开展“伐木节”、“矿工月”等活动,在一定时期内对特定几种物品赋予\iota(t) > 1的特别物价指数,从而实现刺激玩家在特定期间内收集指定物品、提升特定物品的流通量、增加服务器经济活力等目的。
完成最后一块拼图——收购清单和参数的确定
完成了上述所有数理模型的理论后,确定收购物品的清单和参数成为了仅剩的问题。为了玩家们能够全方位发展,我们当然希望尽可能收购更多种类的物品。
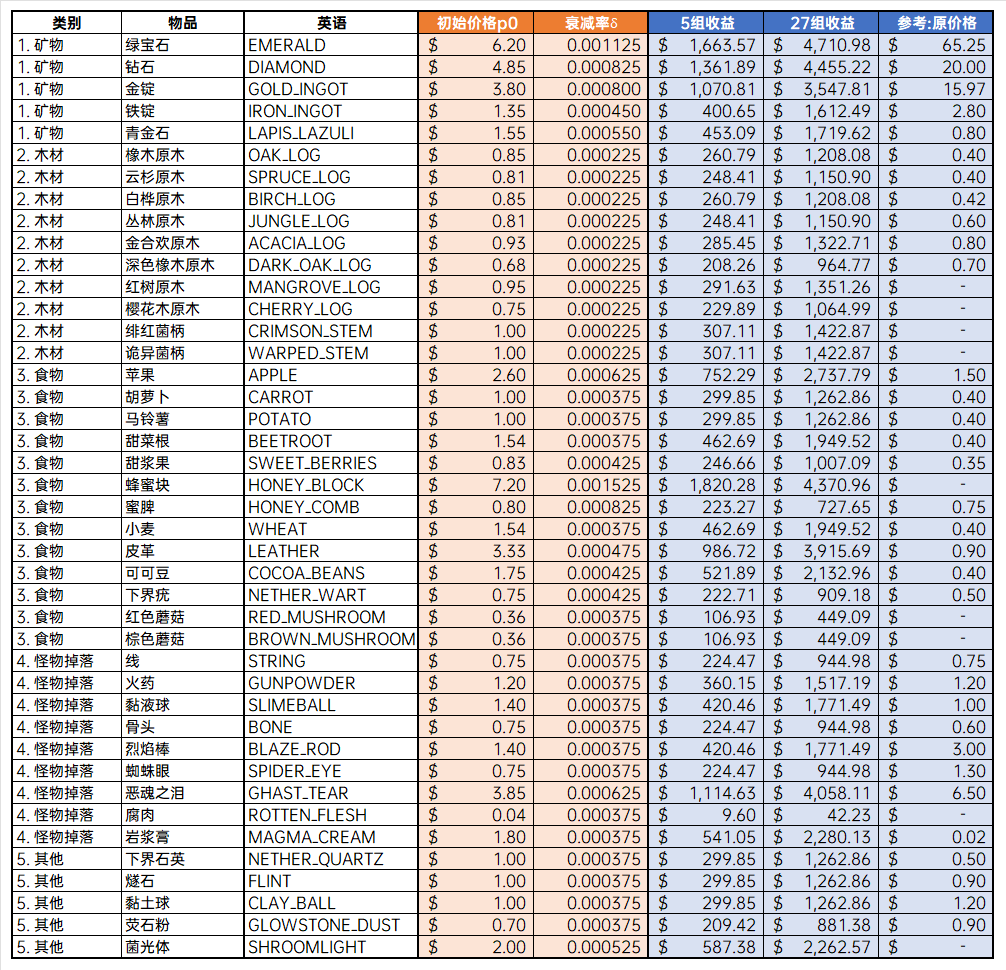
然而,十分遗憾的是,出于种种考虑,我们最终确定出了一份如图5所示的仅包括42个物品的收购清单。我们确定商品清单时,着重考察了各个物品的如下方面:
- 这个物品是否在其他DC玩法中发挥着举足轻重的作用?
- 这个物品是否在日常建设、生产中发挥着重要作用?
- 这个物品是否可以通过自动化红石机械大规模生产?
- 这个物品的获取难度如何?
- ……
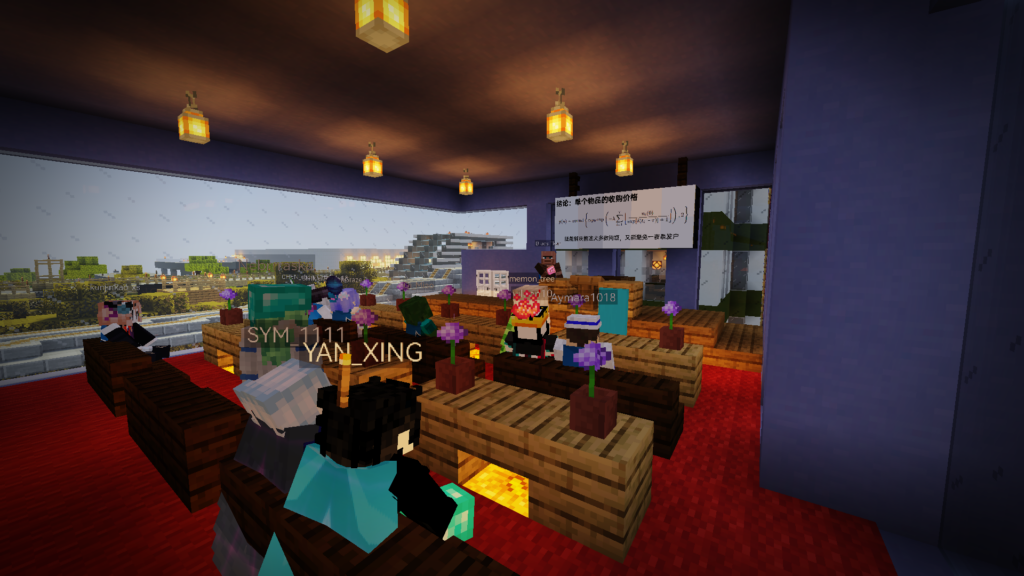
特别需要指出的是,身为DC管理员,我常年以来以创造模式服务DC的各位玩家,因此仅靠我一个人的想法去决定收购清单和参数显然是不合理的。因此,我们通过在游戏里召开多次语音会议征询生存玩家的建议、询问有数理基础的玩家的意见(图6),结合服务器管理组的想法后,最终确定了最终的清单。而在第3代收购系统正式投入使用前,我们还特别邀请了生存玩家前来参加系统的内测(图7)。这一系列看似繁琐的流程,无一例外是为了营造一个科学、合理、公平的环境,无一例外是为了让生存玩家们的利益最大化,无一例外是为了让更多的玩家们参与到新系统的开发,凝聚DC玩家们的所有智慧,共同打造出一个精益求精的收购系统。

总结
第3代收购系统根据玩家在一个周期内的活跃程度,为每位玩家分配下个周期内的收购额度。与第2代收购系统相同,第3代收购系统的周期可定为一个星期。由于玩家不再需要拥抢收购总额度,服务器方面也无需在一周内的特定时间进行收购活动,而是设立长达整整一周的收购时间,让玩家放心出售物品。
根据本改进方案,由于服务器将设置长达一周的收购时间,玩家不再需要拥抢收购总额度。因此,之前因网络不稳定或手速较慢导致无法通过收购系统获取DC币的玩家,可在本改进方案下的收购系统成功进行出售操作,从而获得DC币。这也同时可以减缓未售出物品的积压现象。
再者,第3代收购系统根据某位玩家的某个物品的售出总量不断下调该玩家的该物品的收购价格,可以鼓励玩家收集更多其他种类的物品,可进一步减缓物品积压现象。然而,为了使得该措施取得成效,必须合理设置上文中提到的一系列常数,使得单个玩家的某个物品的收购价格p不易反弹回原有的水平。
此外,由于每位玩家在一个周期内的收购额度是根据上个周期内的活跃系数来决定的,因此也可促进更多玩家登录服务器游玩。当然,考虑到DC玩家大多数为学生,在开学期间通过增加保底基数的方式,为全服玩家提供较低的收购额度,可保障学生玩家在忙碌的学业之余也可通过该渠道获取一定的DC币。
综上所述,第3代收购系统通过引入基于活跃系数的收购额度分配机制以及历史售出数量动态调整的收购价格机制,旨在优化服务器的经济体系,解决第2代收购系统遗留的问题。通过为每位玩家设定不同的收购额度和物品价格,本方案可有效避免全服玩家抢占收购总额度的情况,并可缓解未售出物品积压的问题。此外,基于活跃程度和时间因素调整价格的机制,还能鼓励玩家多样化出售物品,进而促进服务器的物资流通和经济活跃度。第3代收购系统还考虑了学生玩家群体的上线频率,通过保底收购额度保障他们的参与,确保服务器经济系统的公平性和可持续发展。
鸣谢
- Blues_Tkun、SlinkierApple13、kunjinkao_xs构筑了基础算法;
- Blues_Tkun、kunjinkao_xs开发了脚本,Sun_Yu_Xuan对脚本进行了漏洞排查;
- Qi_Miao、SlinkierApple13、DreamCityToger进行了与物品收集效率相关的调研;
- Blues_Tkun、kunjinkao_xs、Qi_Miao、yileen10、THEFREEMAN、BreakGraze、Oracles42、Sun_Yu_Xuan、Dp_Dk_Fantasy确定了收购物品清单;
- Blues_Tkun、Qi_Miao、yileen10、THEFREEMAN、Sun_Yu_Xuan进行了调参工作;
- SlinkierApple13、John_Lu对本文进行了纠错;
- memon_tree、CHEN_chen_CHEN、Rex、Chen_peipei、Mc_thrombus、ZuiLiu_aaaaab等DC玩家提出了宝贵建议;
- kunjinkao_xs、SlinkierApple13、Qi_Miao、yileen10、BreakGraze、Oracles42、memon_tree、CHEN_chen_CHEN、LuGuan_0、SYM_1111、YAN_XING、PPAP、Aymara1018、Leaf_YOKO、WWWMrNobody、ZuiLiu_aaaaab、Ximu、AwRaiy、123456、wenzn等DC玩家参与了内部测试和启用仪式等活动,并给出了宝贵评价。
One comment